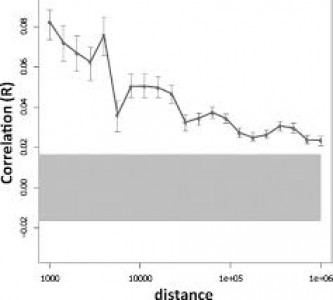
Difference between Association and Correlation
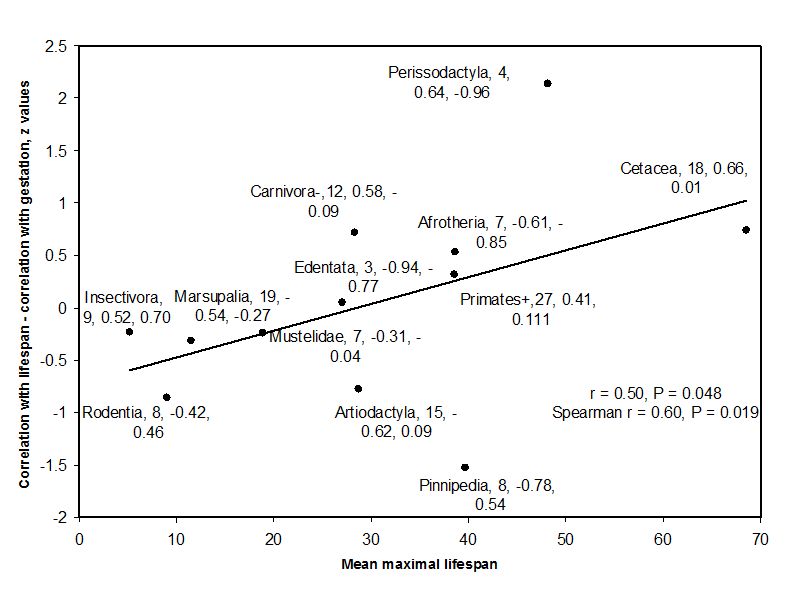
Association and correlation are two terms related to statistical studies. These are actually two different methods of representing a relationship between two statistical variables. Association is a more generalized method of explaining the difference between two statistical terms, while correlation can be considered a special case of the former, where only the linear relationship between two random variables is discussed.
Association is a concept, while correlation is the measurement of association, and there are special tools that are used to measure the magnitude of the latter.
Pearson’s product moment correlation coefficient is used to determine the nature of the relationship between two random variables; that is, whether they are directly related to each other or bear an inverse relationship. It is also used to establish the presence of liner relationships between the variables.
Rank correlation coefficient, on the other hand, is used to determine only the nature of the relationship between the variables, and does not say anything about the linearity of the relationship.
Instructions
-
1
Association
Association, in statistics, is any relationship between two measured quantities (random variables), which makes them statistically dependent. It refers to a broader relationship between the variables, without mentioning the nature of relationship between them (whether they are directly proportional or inversely proportional to each other). Moreover, the relationship between the variables under study should not necessarily be casual.
There are a number of mathematical tools that are used to establish the association between two random variables, including Pearson’s correlation coefficient, distance correlation, odds ratio, Goodman’s and Kruskal’s Lambda, and Spearman’s rho (ρ).
Image courtesy: theanalysisfactor.com
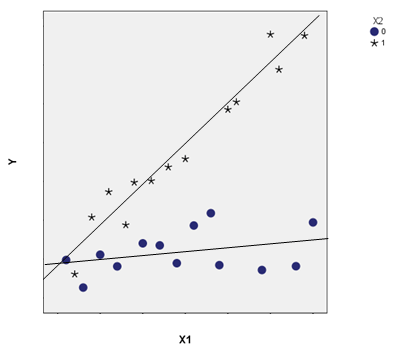
-
2
Correlation
Correlation, in statistics, is defined as the measure of the strength of the relationship between two statistical terms. The correlation coefficient quantifies the degree of change in one random variable due to some change in the other random variable. In statistics, it is connected to the concept of dependence, which refers to any statistical relationship between two random variables or two sets of statistical data.
There are several coefficient correlations used to measure the degree of correlation between two terms, often denoted by ρ (row), Pearson correlation coefficient being the most common one. Its value ranges from -1 to 1 (-1≤r≤+1) and is valid only for linear relationships between random variables. Zero value (0) of r shows that no relationship exists between the two variables, positive value of r shows a positive relationship between the variables, and negative value of r shows a negative relationship between the two variables.
Image courtesy: pnas.org